Fundamentals of Light & Optics
Refraction is the change in direction (bending) of electromagnetic waves due to a change in speed caused by the waves crossing the interface (or boundary) from one medium with a given refractive index into another medium with a different refractive index.
Lets take a look at refractive index in more detail now before continuing our study of refraction.
The index of refraction (or refractive index, RI) is a ratio measure based on speed of light in a vacuum (c) (the reference medium) to the phase velocity (speed of light) in the medium itself.
The maximum speed of light is achived in a vacuum, (299,792,458 m/s), with an index of refraction at exactly 1.0. The index of refraction for air (at 0℃ and 1 atm) is 1.000293, as such, air is also used as a reference as is has very little effect in the refraction of light.
We are able to define the refractive index, (n) using the following equations:
n = c / v
or inversely,
v = c / n
As the speed of light is a constant, the calculated refractive index will be greater than one. However, to note, there are special cases (dependant on frequency) where the refractive index may be smaller than one.
The following table lists some common materials and also some important materials which are used in optics:
| Material | λ (nm) | Refractive Index (RI) |
|---|---|---|
| Vacuum | 1.0 | |
| Air (0°C, 1 atm) | 589.29 | 1.000293 |
| Ice | 589.29 | 1.31 |
| Methanol | 589.29 | 1.3284 |
| Water (20°C) | 589.29 | 1.332986 |
| Ethanol | 589.29 | 1.3614 |
| Ethylene Glycol | 589.29 | 1.4318 |
| Fused Silica & Quartz | 589.29 | 1.4585 |
| Fluorite | 589.29 | 1.433 - 1.435 |
| Pyrex (Borosilicate) Glass | 589.29 | 1.474 |
| Acrylic Glass | 589.29 | 1.489 - 1.492 |
| Optical Crown Glass | 656.3 - 435.8 | 1.52015 - 1.53394 |
| Soda-Lime Glass | 589.29 | 1.518 - 1.520 |
| Flint Glass | 589.29 | 1.523 - 1.925 |
| Quartz Crystal Δn = +0.009 |
589.29 | no = 1.543 - 1.545, ne = 1.552 - 1.554 |
| Sapphire Δn = -0.008 |
589.29 | no = 1.768 - 1.772, ne = 1.760 - 1.763 |
| Cubic Zirconia | 589.29 | 2.15 - 2.18 |
| Diamond | 589.29 | 2.419 |
| Optical Schott Glass | ||
| Borosilicate Crown BK7 | 2325.4 - 351.1 | 1.48921 - 1.53894 |
| Dense Flint SF11 | 2325.4 - 404.7 | 1.73294 - 1.84208 |
| Lanthanum Dense Flint LaSF9 | 2325.4 - 404.7 | 1.80055 - 1.89844 |
| Barium Crown BaK1 | 2325.4 - 351.1 | 1.54556 - 1.60062 |
| Flint F2 | 2325.4 - 351.1 | 1.58465 - 1.67359 |
| Laser Crystals & Hosts | ||
| Ruby Δn = -0.008 |
694.3 | no = 1.763, ne = 1.755 |
| ND:YAG | 800 - 1400 | 1.812 - 1.824 |
| ND:YVO4 Δn = +0.208 Δn = +0.214 Δn = +0.235 |
1064 808 532 |
no = 1.957, ne = 2.165 no = 1.972, ne = 2.186 no = 2.021, ne = 2.256 |
| Specialised Optics For Infrared Wavelengths | ||
| Germanium (Ge) | 550 10.6 um |
2.67 2.40 |
| Zinc Selenide (ZnSe) | 589.29 13.02 um - 2.06 um |
1.7 4.00 - 4.10 |
Notes:
By standards, refractive index measurements are taken at the wavelength of 589.29nm (Yellow), which corresponds to centre wavelength known as D-Line of the Fraunhofer sodium doublet D1 & D2 spectral lines.
Its noted that some of the materials, e.g. Quartz, have two sets of refractive indices, no and ne. These materials exhibit Birefringence or double refraction.
Birefringence causes light waves entering the material to be separated into two wavefronts or rays known as the ordinary ray and the extraordinary ray;- i.e. double refraction. Birefringence can only occur in materials that exhibit a directionally dependant (or anistropic) characteristic.
The difference in index (or magnitude of birefringence) (Δn) of light traveling along the optic axis and light traveling perpendicular to it, can be calculate by subtracting the refractive index of the extraordinary ray (no) from the refractive index of the ordinary ray (ne):
Δn = ne - no

Fig 2.5 demonstrates the basic principle of birefringence. The two refracted rays have a 90° polarisation with respect to each other. The ordinary ray is one that has its polarisation perpendicular to the plain that includes the optical axis, and the extraordinary ray having its polarisation in the plane of the optical axis.
If we rotate the crystal around the optical axis, the position of the ordinary ray will remain stationary, while the extraordinary ray will trace a circular path.
In optics, birefringence widely finds its use in LCD displays, optical modulators, color filters, wave plates, gratings etc. Some of the more important applications are in laser physics, include second harmonic generation (e.g. frequency doubling of ND:YAG laser fundamental 1064nm wavelength to 532nm (green) wavelength) and many other important non-linear optical processes.
Common examples of where we see refraction at work included the appearance of a 'bent' straw in a glass, and how a prism will split white light into its component colours.

As we have learnt, light waves travel at different speeds in different mediums of given refractive indices. At the boundary of a medium with a higher index of refraction, the wave front will change direction towards the normal due to a change in the wave's phase velocity caused by the materials refractive index.
This effect will also occur in the opposite direction;- i.e. from a high RI material to a low RI material, with the change of direction being away from the normal;- i.e. the wave speeds back up as it crosses the boundary.
As refraction causes a change in the speed (velocity, v) of the wave, the frequecy (f) and wavelength (λ) can change independantly. When light is refracted, the wavelength changes, but its frequency remains constant;
λ = v / f
If light travelling in a medium with a refractive index of n1 strikes the surface of a material with a refractive index of n2 at an angle of θ1 to the normal, the light direction in the second material is given by θ2 in the equation:
n1 sin θ1 = n2 sin θ2
This equation is known as Snell's law of refraction.
Snell's law states that:
"The ratio of the sines of the angles of incidence and refraction is equal to the ratio of velocities in the two media, or equal to the opposite ratio of the indices of refraction."

As we have just learnt, as light passes through one medium to another, this causes light to refract, As we also have learnt from light theory, white light is actually composed of many separate wavelengths (or colours)., refraction will cause the waves to change direction.
If we shine a beam of white light through a prism, we will see white light being separated into components of different wavelegnths and we see a 'rainbow'.
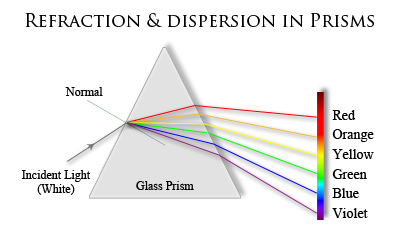
Refraction alone is not responsible for the separation of light in a prism, what is responsible is a phenomenon known as dispersion. The separation of light in a prism is known as chromatic dispersion. Chroma comes from the Greek, meaning colour.
Taking a brief look at dispersion; -
This relates to the phase velocity of a wave being dependant on its frequency, - i.e. any one frequency component. We also have group velocity dispersion (GVD), which is the overall shape of a wave's amplitude (or envelope) containing different Wavelength components.
GVD is most problematic in the field of fibre optics, where it causes light pulses to spread, degrading signals over long distances.
There are three types of dispersion encountered in optics;-
- Material Dispersion
- Waveguide Dispersion
- Modal Dispersion
Material dispersion is the frequency-dependant response a material has to waves propagating through the material. Material dispersion is responsible for separation of light in a prism. Desired applications include spectrometers, used to analyse spectal wavelengths. The undersired effect of material dispersion is in lenses, known as chromatic aberration.
We are able to calculate the phase velocity v of a wave in given uniform medium and known refractive index from our previous equation:
v = c / n
Referring back to our example of a prism separating white light into its component wavelengths, and also our look at Snell's law, we are now able to understand the physics involved.
Referring to Snell's law, we see that the angle of refraction of light in a given material, in our case we will use the prism, depends on the refractive index of the material (prism glass).
Let's now use a real-life data to calculate the angles of refraction in a prism, to see how a prism (or other optical element such as a lens) causes chromatic dispersion.
We are going to use Optical Crown Glass as our sample, and an angle of incidence, n1 of 40°. Using a material datasheet (available from CVI Laser Optics), we are able to obtain the refractive indices of optical crown glass at specific wavelengths.
With the use of Algebra to re-write Snell's equation, we can now substitute the values into the equation:
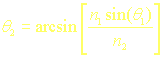
| Colour | λ (nm) | RI (n2) | Angle of Refraction |
|---|---|---|---|
| Red | 656.30 | 1.52015 | 25.0143° |
| Orange | 589.00 | 1.5228 | 24.9678° |
| Yellow | 587.60 | 1.52288 | 24.9664° |
| Green | 546.10 | 1.52501 | 24.9292° |
| Blue | 480.00 | 1.5296 | 24.8493° |
| Violet | 435.80 | 1.53394 | 24.7742° |
Using Fig 2.7 as a reference, we can now see from the results of our calculation, the blue wavelength, being the shortest, and also having the highest index of refraction (n2) in the given material, is refracted (bent) more strongly with an angle of 24.7742° with respect to the normal, which is in contrast to the red wavelength with an angle of 25.0143° with respect to the normal.
Waveguide dispersion depends on the geometrics, design and chemical composition of the waveguide itself and the different propagating wavelengths, causing a distortion of pulses propagating in waveguides.
Modal dispersion, also causes a pulse distortion effect, or pulse spread over time due to the propagation velocity (speed) of the signal traveling in the fibre is not the same for all of the modes. For simplicity of understanding, a mode relates to the oscillation of a wave.
Waveguide and modal dispersion relate to undesired effects in optical fibres that result in pulses spreading (or stretching) and ultimatly the degradation of signals.
We now conclude this section by taking a closer look back at total internal reflection.
Total internal reflection occurs when light crosses the boundary from a medium with a higher refractive index than the medium its traveling into at a greater angle than the critical angle with respect to the normal.
The critical angle is the angle of incidence above which a ray of light will cease to be transmitted and will be totally reflected back into the medium.
At the critical angle, a ray of light will travel along the boundary or interface of two materials.
Below the critical angle, and the ray of light will be transmitted through (undergoing normal refraction), as well as a small pecentage of the ray reflected back into the material.

Referring to Fig 2.8, n1 has a higher refractive index than n2. For angle θi2 greater than the critical angle, θc, the ray is totally reflected back into the material. For angles (θi1) less than θc, the ray is both partially transmitted as well as being partially reflected back into the material.
We are able to calculate the criticle angle, θc;
θc = (n2 / n1)
Where n1 and n2 are the refractive indices of the materials.
For calculated values where n2 / n1 is greater than 1 the arcsine is not calculated and therefore total internal reflection does not occur.
To use a some real-life data as an example, we can calculate the critical angle. We will select Borosilicate crown BK7 glass as our sample, and will will use a reference wavelength of 632.8nm (Helium-Neon Laser). Referring to material specifications from CVI Laser Optics, The index of refraction of BK7 at a wavelength of 632.8nm is 1.51509, using this as our value for n1 and 1.00 (air) as our n2 value, we calculate the critical angle, θc:
θc = arcsine (1.00 / 1.51509) = 41.30°
For angles of incidence above 41.30° total internal reflection will occur.
Total internal reflection plays an important role in optical fibres as its the function with which allows light to propagate down the fibre (a waveguide). We also find total internal Reflection in binoculars, cameras and any other piece of equipment using prisms.
In the next section, we will discuss the property of diffraction.
This Document Complies to W3C XHTML 1.0 Strict Standards



